Der LC-Schwingkreis dient in der Hochfrequenztechnik zur Filterung oder Generierung von Frequenzen. In diesem Artikel geht es um die Grundlagen und um die Berechnung von einem LC-Schwingreis. Es handelt sich hierbei um einen passiven Schwingkreis, der nach dem Anstoß kurz schwingt, bis die Energie aufgrund der Verluste vollständig aufgebraucht ist. In einem weiteren Artikel wird es um einen aktiven LC-Schwingkreis gehen, der selbstständig weiter schwingt und somit als LC-Oszillator verwendet werden kann.

Der Parallelschwingkreis

Der Parallelschwingkreis besteht aus einer Spule und einem Kondensator. Lädt man den Kondensator auf und schließt ihn dann parallel an die Spule an, so fließt die Energie vom Kondensator in die Spule. Kurze Zeit später fließt die Energie von der Spule wieder zurück in den Kondensator, aber diesmal in umgekehrter Stromrichtung. Der Kondensator wird mit umgekehrter Polung aufgeladen und kurze Zeit später beginnt der Kreislauf wieder von vorne. Man spricht hier von einem freien Schwingkreis, der theoretisch seine Schwingung unendlich lange fortsetzen würde, wenn der Schwingkreis nicht verlustbehaftet wäre. Die folgende Grafik zeigt einen praktischen Vergleich des elektrischen Schwingkreises mit einem Pendel:

Im ersten Bild (1) ist der Stromkreis offen und der Kondensator geladen. Unterhalb sieht man ein Pendel in linker Position. Schließt man den Stromkreis, so fließt der Strom fast linear ansteigend zur Spule und die Spannung im Kondensator baut sich ab (2). Das untere Pendel schwingt jetzt von links zur Mitte. Sobald die Spannung im Kondensator komplett abgebaut ist, liegt die gesamte Energie in der Spule. Anschließend beginnt der Strom wieder von der Spule zum Kondensator zurückzufließen. Es entsteht eine Gegenspannung, die den Kondensator langsam, aber mit umgekehrter Polung wieder auflädt (3). Das Pendel bewegt sich während der Aufladung des Kondensators weiter nach rechts. Ist der Kondensator voll aufgeladen, liegt die maximale Spannung an und es fließt kein Strom mehr. In diesem Moment fängt der Strom wieder an, in die Spule zu fließen (4). Das Pendel bewegt sich wieder zur Mitte, wo sich wieder die gesamte Energie in der Spule befindet. Es findet wieder eine Stromumkehr in der Spule statt und der Kondensator wird wieder in umgekehrter Polarität geladen. Befindet sich die gesamte Energie wieder im Kondensator, so ist Ausgangszustand von Bild 1 erreicht und die nächste Schwingung beginnt.

Verluste im Schwingkreis

Leider schwingt der LC-Kreis in der Praxis nur sehr kurz und mit jeder Schwingung nimmt die Amplitude ab, sodass er letztendlich nach einer bestimmten Zeit zum Stillstand kommt. Die Verluste entstehen insbesondere am ohmschen Widerstand aller Leitungen und am Spulendraht. Verluste können aber auch magnetisch über den Spulenkern oder durch eine elektromagnetische Abstrahlung entstehen. Grundsätzlich kann man alle Verluste einen parallelen Widerstand (R) zuordnen:

Parallelschwingkreis berechnen

Der Parallelschwingkreis besteht aus zwei Komponenten, nämlich dem Kondensator (C) und der Spule (L). Je nachdem, wie sich zumindest einer dieser Parameter ändert, ändert sich auch die Resonanzfrequenz. Mit der Thomsonsche Resonanzformel kann die Frequenz eines LC-Schwingkreises berechnet werden:

Praktischer Versuch

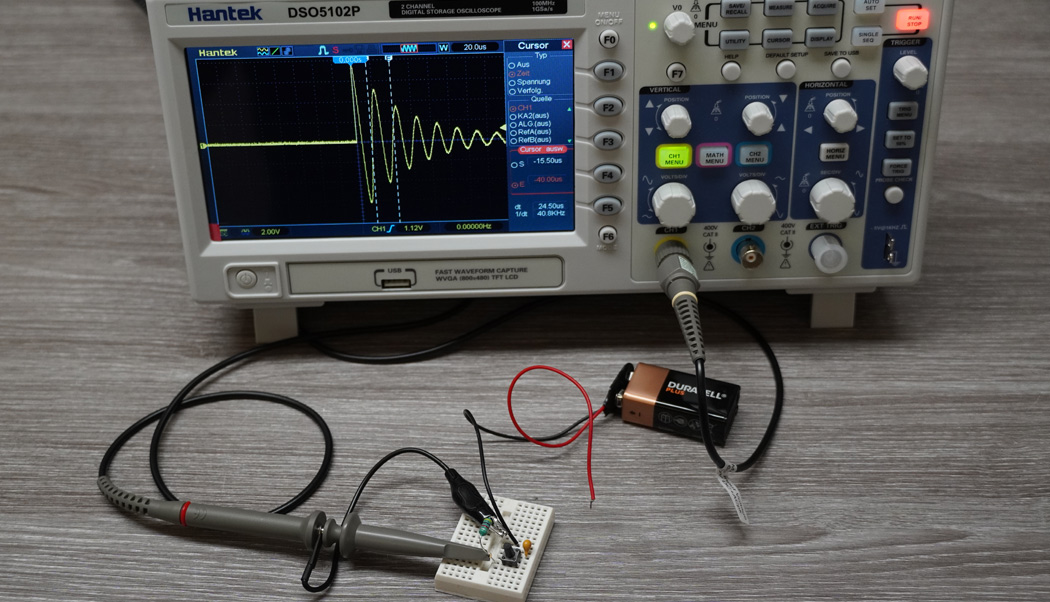
Um die zuvor erwähnten Abläufe, Verluste und die Genauigkeit einer Berechnung zu analysieren, gibt es ein praktisches Beispiel. Gegeben ist eine Spule mit 4,7 Millihenry und ein Kondensator mit 3,3 Nanofarad. Zuerst wird daraus die Resonanzfrequenz des Schwingkreises berechnet. Der Versuchsaufbau besteht aus einem LC-Glied mit einem Taster (Schließer). Zuerst wird der Kondensator extern auf etwa 8 Volt geladen und anschließend mit dem Taster parallel zur Spule geschaltet:

Am einfachsten ist die Berechnung, wenn man Kapazität und Induktivität in die Basiseinheiten Farad und Henry umwandelt und direkt in die Formel einsetzt. Das Resultat ist die Resonanzfrequenz in Hertz. Folgender Screenshot zeigt die freie Schwingung kurz nach Zusammenschluss von L und C:

Am Oszilloskop sieht man, wie die Spannung steil nach oben geht. Anschließend bildet sich ein schöner Sinus, wo die Amplitude mit jeder Schwingung deutlich abnimmt. Nach nur wenigen hundert Mikrosekunden ist die Energie aufgrund der Verluste vollständig aufgebraucht und der Schwingkreis bricht zusammen. Wie auf den Screenshot deutlich zu sehen ist, ändert sich zwar die Amplitude, aber nicht die Frequenz. Laut Oszilloskop beträgt die Frequenz 44,4 kHz und stimmt mit der Berechnung exakt überein. Es ist jedoch in der Praxis vollkommen normal, dass die Berechnung um mehrere Hundert Hertz abweichen kann. Dies liegt u. a. auch an den Toleranzen der verwendeten Bauteile.

Kapazität/Induktivität berechnen

Häufig hat man eine bestimmte Frequenz, die man mit einem LC-Schwingreis erreichen möchte. Idealerweise kennt man die Induktivität und errechnet sich mit der Formel die passende Kapazität. Umgekehrt kann man auch zum Kondensator die passende Induktivität berechnen.

In der Praxis findet man meistens nicht die exakten Bauteilwerte und setzt somit auf veränderbare Bauteile. Generell ist es besser, wenn man den Kondensator durch einen Drehkondensator ersetzt. Große Drehkondensatoren sind heutzutage ohnehin Mangelware, daher muss man meistens zum festen Kondensator noch einen kleinen Drehkondensator parallel schalten. Veränderbare Kondensatoren sollten gegenüber den veränderbaren Spulen bevorzugt werden, da sie eine höhere Güte aufweisen.